Let’s break down what you can expect on the GRE Quant section so you can dive into practice with confidence.

01. Format & Timing

You'll complete two scored Quantitative Reasoning sections on test day. Both sections cover the same math topics, but they serve different purposes:

Section 1: Sets the Baseline

• 12 questions | 21 minutes
• A mix of all question types
• Determines the difficulty level of Section 2
• Your goal: Focus on accuracy with steady pacing

Section 2: Adapts to You

• 15 questions | 26 minutes
• Difficulty adjusts based on your Section 1 performance
• If it feels harder, that’s a good sign- you're doing well!

Your goal: Stay calm and sharp through the challenge

02. What Math Does It Cover?

The GRE Quant section tests high school-level math.

Here's what you'll see:

• Arithmetic: Fractions, ratios, percentages
• Algebra: Equations, inequalities, expressions
• Geometry: Angles, shapes, coordinate geometry
• Data Analysis: Graphs, probability, statistics

The real challenge isn’t just the math- it’s how questions test your logical thinking and problem-solving skills, not just your ability to plug into formulas.

‍01. GRE Quantitative Comparison Questions (QC)

Quantitative Comparison questions present you with two quantities, labeled “Quantity A” and “Quantity B,” and your task is to compare them. You don’t have to find exact values; instead, you choose one of four standard answer choices:

1. Quantity A is greater.
2. Quantity B is greater.
3. The two quantities are equal.
4. The relationship cannot be determined from the information given.

In other words, you decide whether A > B, A < B, A = B, or if there’s not enough info to tell. These questions are tricky because they often look like you should do a lengthy calculation, but there’s usually a shortcut or comparison strategy.

Sample Quantitative Comparison Questions:

Q1) Quantity A: 50² + 60² + 90²

Quantity B: (50 + 60 + 90)²

Which is greater, Quantity A or Quantity B?

Answer: Quantity B is greater.

Explanation:

Step 1) At first glance, you might consider calculating each quantity, but that’s a lot of arithmetic – and a perfect example of where a QC shortcut helps.

Notice that (50 + 60 + 90)² would expand as 50² + 60² + 90² + 2(50 ∗ 60 + 50 ∗ 90 + 60 ∗ 90).

Step 2) That expansion includes all the terms in Quantity A plus additional positive terms.

Specifically, Quantity B = 50² + 60² + 90² + 2(50 ∗ 60 + 50 ∗ 90 + 60 ∗ 90).

Step 3) Those extra terms 2ab are all positive, which means (50 + 60 + 90)² must be larger than the sum of the squares alone.

Without crunching any numbers, we can safely conclude Quantity B > Quantity A, so the answer is (B).

Q2) Given that a and b are positive integers and a² = b³:

Quantity A: a

Quantity B: b

Which is greater?

Answer: The relationship *cannot be determined* from the information given.

Explanation:

The equation a² = b³ links a and b, but there could be multiple

pairs of integers that satisfy this equation. We are told both are positive integers. One approach is to find prime factorizations or try small numbers.

For instance, a = 8, b = 4 works because 8² = 64 and 4³ = 64.

In that case, a =8 and b = 4, so Quantity A > Quantity B.

However, another solution is a =1, b = 1 (trivially, 1² = 1³), where a = b.

02. GRE Multiple-Choice Questions (Single Answer)

Multiple-choice questions with a single answer are what most of us think of as standard math problems. A question is posed, usually as a word problem or an equation to solve, and five answer choices (labeled A through E) are given. Only one choice is correct.

Difficulty of these questions ranges from easy definitions to very tricky multi-step problems. The key here is to solve efficiently and avoid common trap answers.

Sample Multiple-Choice Question:

Q1) The price of a pair of shoes was :80 last week. On January 1st, the store increased the price by 20%. Later, an employee purchased the shoes using a 10% employee discount on the new price. What price did the employee pay?

1. $70.40
2. $82.00
3. $83.33
4. $86.40
5. $88.00

Answer: $86.40 (Choice D) is the amount the employee paid.

Explanation:

Let’s break it down step by step:

Step 1) Original price = $80.

Step 2) After a 20% increase,

the new price = original price * 1.20 = $80 × 1.20 = $96.

So the shoes were marked at $96 post-increase.

Step 3) The employee gets a 10% discount on that $96. A 10% discount means the employee pays 90% of the price (because they save 10%).

Another way: Employee price = $96 * 0.90.

=$96 × 0.90 = $86.40.

So the final cost to the employee is $86.40.

Looking at the answer choices, $86.40 corresponds to choice (D).

Check for reasonableness:

If you accidentally applied the discounts in the wrong order or combined percentages incorrectly, you might see other answer choices.

For example, $70.40 (A) might result from taking 10% off the $80 then adding 20%, which is mixing up the order. The GRE often includes such trap answers for test-takers who misread or mis-sequence the steps. Always apply percentage changes one at a time carefully.

Multiple-Choice Tip:

‍Translate word problems into equations or logical steps. Here, price changes can be handled with multiplier factors (increase 20% = ×1.2, decrease 10% = ×0.9). Using these multipliers prevents confusion that can arise from adding/subtracting percentages in absolute terms.

Also, be wary of answers that look “too neat” – they might be there to lure you from a small mistake.

Let’s try another one, involving a bit of algebra:

Q2) If 6k² + k = 2 and k > 0, what is the value of k?

1. ^1/2
2. ^3/2
3. 2
4. 3
5. No positive solution exists

Answer: 1/2

Explanation:

We have a quadratic equation 6k² + k − 2 = 0.

To solve for k, it might be easiest to use the quadratic formula.

First, compute the discriminant: 1 − 4(6)(−2) = 1 + 48 = 49.

The square root of 49 is 7.

So, discriminant= (−1±7)/12

This gives two solutions k=½ or -⅔..

The second solution is negative (−0.667), but we’re given k > 0. Therefore, we discard the negative root.

The positive solution is k = 1/2 That corresponds to choice (A).

03. GRE Numeric Entry Questions

Numeric Entry questions are those where you must come up with the answer yourself and type it in, rather than selecting from given choices. There are no multiple-choice options to guide you – and no chance to guess from provided choices.

On the GRE, you’ll see a small box (or sometimes two boxes if a question requires, say, a fraction or two-part answer) where you enter your response.

The upside is there’s no trap of selecting the wrong choice; you either get it right or not.

Sample Numeric Entry Question:

Q1) Renaldo earns a monthly base salary of 2,500 plus a commission equal to 10.5% of his total sales for the month. If in a certain month Renaldo earned

:3,025 in total, what were his total sales that month? (Provide your answer as a whole number.)

Answer: 5000$

Explanation:

Step 1) Renaldo’s earnings come from two parts: salary + commission.

We know salary = $2,500.

Step 2) Let S = total sales for the month.

Commission is 10.5% of S, which as a decimal is 0.105 × S.

Step 3) The equation for total earnings E in a month is:

E = salary + commission = 2500 + 0.105S.

Step 4) We’re given E = 3025.

So:

2500 + 0.105S = 3025.

Step 5) Subtract 2500 from both sides: 0.105S = 525.

‍Step 6) Now divide both sides by 0.105 to solve for S.
You could do this by hand or use the on-screen calculator.

525/0.105 = 5000 (since 0.105 × 5000 = 525).

Therefore, Renaldo’s total sales were $5,000.

When entering your answer, you’d just type 5000 (the GRE does not require the dollar sign in numeric entry).

Numeric Entry Tips

1. Be Precise: Double-check your setup and calculations- no answer choices to guide you.
2. Use the Calculator Wisely: Good for messy math, but verify key steps.
3. Sense-Check Your Answer: Ask if it’s reasonable (e.g., 10% of $5,250 ≈ $525, so $5,000 in sales makes sense; $500 or $50,000 doesn’t).

Q2) At a dog show, there are 5 finalists competing for “Best in Show” and “Honorable Mention” awards. One dog will get Best in Show, and a different dog will get Honorable Mention. How many different ways can these two awards be given out? (Provide your answer as an integer.)

Answer: 20$

Explanation:

We have 5 finalists and we need to choose 2 distinct winners: one for Best in Show and one for Honorable Mention. This is essentially an ordered selection (because getting Best vs. Honorable is different).

There are a couple of ways to reason:

Think of it step by step: Choose the Best in Show first (5 possible dogs), then choose Honorable Mention from the remaining dogs (4 possible, since one has already won Best in Show).

Using the multiplication principle: 5 × 4 = 20 possibilities.

Alternatively, recognize this as a permutation: The number of ways to pick 2 winners out of 5 where order matters is P (5, 2) = 5 × 4 = 20.

Either way, the answer is 20. If order didn’t matter (say, two dogs just tied for some prize), we’d divide by 2, but here the awards are distinct, so order does matter.

Numeric Entry Tip:

For counting problems, break them into stages (as we did) or use combinations/permutations formulas if you remember them. Ensure you’re clear on whether order matters.

04. GRE Multiple-Answer Questions (Select All That Apply)

Multiple-answer questions are a subset of problem-solving questions where more than one answer choice may be correct. Typically, you’ll see a prompt like “Select ALL such answers that apply” or “Select two answers” etc.

The GRE will usually hint at how many correct choices there are (e.g. “Indicate all such values” often means multiple selections, or sometimes they explicitly say “Select two answers”). If not, you must consider the possibility of multiple correct answers.

Sample Multiple-Answer Question:

Q1) A population of chickens has an average (mean) weight of 6.3 pounds, with a standard deviation of 1.2 pounds. Which of the following weights (in pounds) are within 1.5 standard deviations of the mean? (Select ALL that apply.)

Choices: 4.4, 4.6, 5.1, 5.2, 6.9, 7.6, 7.7, 8.2

Answer: 4.6; 5.1; 5.2; 6.9; 7.6; 7.7 are within 1.5 standard deviations.

Explanation:

Step 1) 1.5 standard deviations is 1.5 × 1.2 = 1.8 pounds. “Within 1.5 SD of the mean” means we go 1.8 pounds below and above the mean as our range.

Step 2) The mean is G.3, so:

Lower bound = 6.3 − 1.8 = 4.5.

Upper bound = 6.3 + 1.8 = 8.1

Step 3) Any chicken weight in this population between 4.5 and 8.1 (inclusive) would be within 1.5 SD of the mean. Now let’s check the list:

• 4.4 – this is slightly below 4.5, so it is more than 1.5 SD away (too low). Exclude 4.4.
• 4.6 – this is above 4.5, so it’s in the range. Include 4.6.
• 5.1 – in range (>=4.5 and <=8.1). Include.
• 5.2 – in range. Include.
• 6.9 – in range. Include.
• 7.6 – in range. Include.
• 7.7 – in range (7.7 <= 8.1). Include.
• 8.2 – this is slightly above 8.1, so it’s just outside the range. Exclude 8.2.

Step 4) So the weights that qualify are 4.6, 5.1, 5.2, 6.9, 7.6, and 7.7. You would select all six of these choices.

Multiple-Answer Tip: Treat the condition separately for each choice and don’t ignore borderline cases. In our case, 4.5 and 8.1 were the cutoffs; if any choice had exactly 4.5 or 8.1, it would count as “within” the range (assuming inclusive interpretation). Always double-check if the phrasing implies inclusive or exclusive bounds – “within 1.5 SD” typically includes those exactly at 1.5 SD. If unsure, err on the side of including the boundary values unless told “strictly within.”

Also, check all options. It sounds obvious, but under time pressure some students stop after finding a couple of correct answers. Don’t leave any correct choice unmarked. Conversely, be cautious not to mark an appealing but incorrect choice – there’s no partial credit, so accuracy matters.

Q2) If x>0x>0, which of the following expressions are equal to 3.6% of 5x/12​?
(Select ALL that apply.)

Choices:

1. A. 3 percent of 20x
2. B. x percent of 3/2​
3. C. 3x percent of 0.2
4. D. 0.05 percent of 3x
5. E. 3x/200

(Note: “y percent of z” means [(y/100)×z]

Solution: Choices B and E are correct (they equal 3.6% of 5x12​).

Explanation:
Step 1) First, let’s simplify what “3.6% of (5x/12)​” equals in a cleaner form.
Convert 3.6% to a decimal:
3.6% = 0.036.
Step 2) Now multiply by 5x12​:

0.036×(5x/12)= 0.036×(5x/12)= 0.18x/12=0.015x

0.036×5x/12= {0.036×(5x/12)}/12 = 0.015x

Step 3) We can also express 0.015 as a fraction:

0.015=15/1000=3/200

So 0.015x=3x2000.015x=2003x​.
Step 4) This means 3.6% of 5x/12 simplifies to 3x/200

Great- now we just need to see which choices match 3x/200.

Step 5) Let’s interpret each choice:

• A. 3 percent of 20x = 0.03×20x=0.6x
   That’s 0.6x, not 3x2002003x​.

So A is out.

• B. x percent of 3/2​

Aha! This is exactly 3x2002003x​.

Include B.

• C. 3x percent of 0.2

That’s 0.006x, not 0.015x.

Exclude C.

• D. 0.05 percent of 3x
   
  That equals 0.0015x, not 3x/200.

Exclude D.

• E. 3x/200​ is already exactly in the form we found.

Include E.

Multiple-Answer Tip:

‍Converting everything into a common format (decimals or fractions) can help on percent problems. Also, read carefully: choice B said “x percent of (3/2)” – it’s easy to misread these kinds of statements under pressure.

05. GRE Data Interpretation Questions (Charts & Graphs)

Data Interpretation (DI) questions are a subset of GRE Quant that present data in the form of charts, graphs, tables, or other visual formats, followed by one or more questions about that data.

On the GRE, typically you’ll see a small set of, say, 2–3 questions all referring to the same data presentation. They are essentially still multiple-choice questions (sometimes numeric entry) but with the added challenge of interpreting the information correctly from the graphic.

Sample Data Interpretation (DI) questions:

Q1)

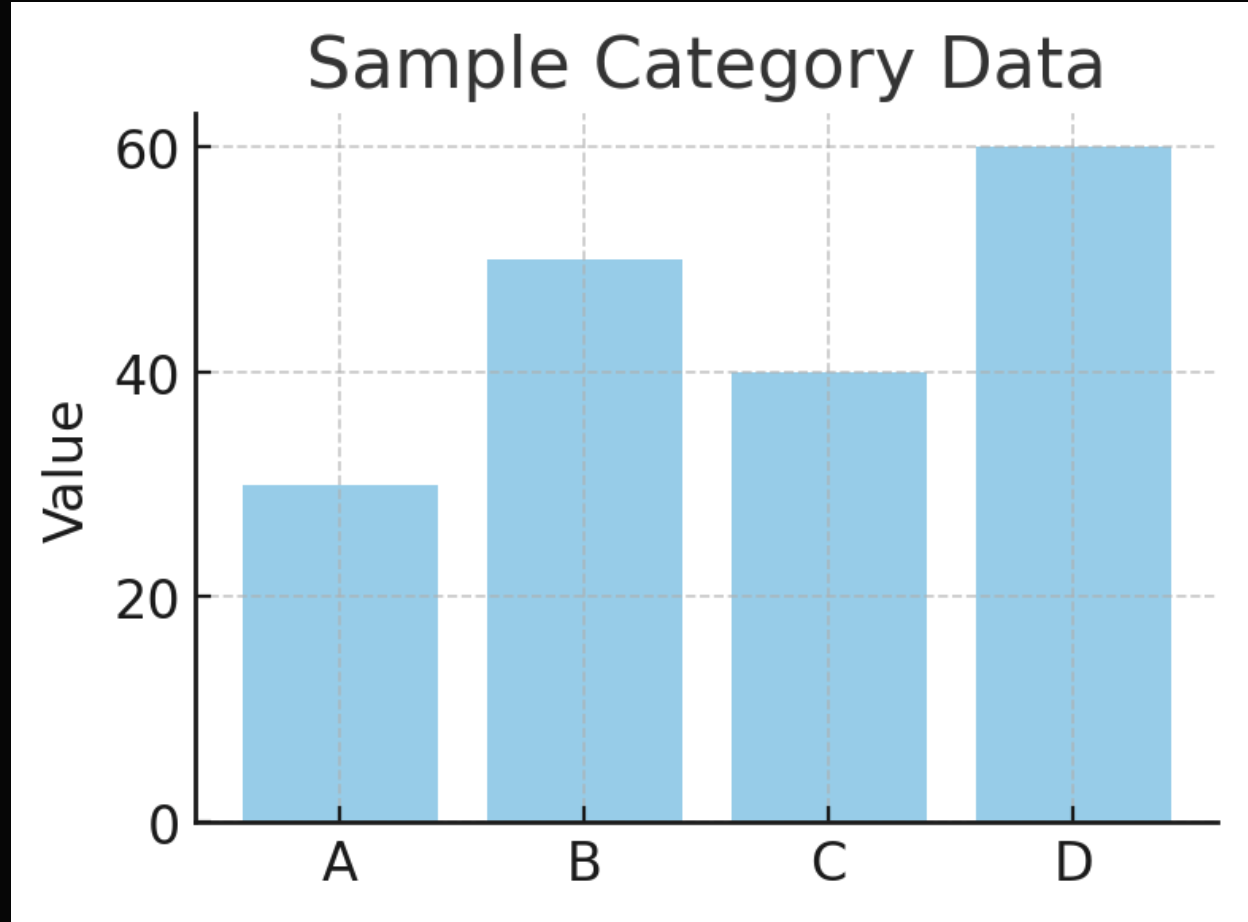
Sample Data Interpretation Chart: Values for Categories A, B, C, and D.

Based on the chart above, which category’s value is approximately 33% of the total of categories A, B, C, and D?

(A) A

(B) B

(C) C

(D) D

Answer: C (Category C).

Explanation:

Step 1) From the sample chart, the values are roughly: A ≈ 30, B ≈ 50, C ≈ 40, D ≈ 60 (as shown on the y-axis).

Let’s first find the total of all categories:

30 + 50 + 40 + 60 = 180.

Now, 33% (which is one-third) of 180 is (⅓) 180 = 60. We’re looking for which category’s value is about 60, since 60 is roughly 33% of the total.

Step 2) Category D is exactly 60 in this chart, but let’s double-check the phrasing: it says “approximately 33%”. Category C is 40, which is about 22% of the total, not 33%. Category B is 50 (about 28%). Category D is 60 (which is one-third).

Category A is 30 (about 17%).

The closest to one-third is Category D at 60.

However, notice category D is exactly 60 which is one-third of 180.

So D is the clear answer. If the values were slightly different, we’d choose the one nearest to 60.

01. Quantitative Comparison (QC) – Think Fast, Not Exact

These questions test your ability to reason rather than calculate. Don’t waste time crunching numbers when logic will do.

Top Strategies:

• Use Algebraic Identities: Recognize identities or common factorizations to simplify.
• Avoid Full Math: If exact values aren’t needed, don’t compute them. Look for structure and symmetry.
• Plug in Easy Values: Try 0, 1, -1, 2, or fractions for variables to test different scenarios.
• Try Multiple Cases: If some values make A > B and others reverse it, the answer is (D) Cannot determine.
• Spot Extra Positive Terms: If B = A + something positive → B is greater.
• Check Signs: When variables are unrestricted, try both positives and negatives.
• Know the Answer Choices: Familiarize yourself with (A) A > B, (B) B > A, (C) A = B, (D) Cannot determine.

02. Multiple-Choice – Single Answer: Work Smart, Not Just Hard

Each question has one correct answer — so aim for efficient problem-solving, not brute force.

Top Strategies:

• Show Your Work: Write steps to avoid small mistakes, especially in multi-step algebra or geometry.
• Watch the Clock: Stay methodical but pace yourself — efficiency matters more than perfection.
• Use Backsolving: Start with Choice C in numerical questions and work backward.
• Estimate When Appropriate: Use rough math to eliminate unrealistic choices quickly.
• Eliminate Incorrect Answers: Cross off anything clearly too big, too small, or logically wrong.
• Recheck If Needed: If more than one answer seems correct, something’s likely off — revisit the problem.

03. Numeric Entry: No Help from Answer Choices

Here, you’re completely on your own — no multiple choice means no hints. Precision is key.

Top Strategies:

• Be Exact: No choices means no second-guessing — your answer must be spot-on.
• Write Steps Out: Prevent tiny mistakes by clearly laying out your math.
• Verify Your Solution: Plug it back into the problem to confirm.
• Follow Input Format: Enter decimals, fractions, or whole numbers exactly as requested.
• Be Meticulous: Mis-entering a digit or sign can cost you the question.

04. Multiple-Answer Questions: All or Nothing

Select all correct choices — and none of the incorrect ones — to earn full credit.

Top Strategies:

• Understand the Question: Read carefully — are you selecting two? All that apply? Don’t skim.
• Evaluate Each Choice Separately: Don’t assume patterns — assess each on its own merit.
• Follow Instructions Exactly: If told to select two, only select two.
• Aim for Completeness: One wrong or one missed choice = zero credit.
• Review Your Selections: Quickly re-check if time permits to ensure you didn’t miss something subtle.

05. Data Interpretation: Graphs and Tables Done Right

Often underestimated, these visuals can trip you up if you’re not methodical.

Top Strategies:

• Check Scale and Units: Don’t assume — verify thousands, millions, or percent.
• Don’t Eyeball It: Read exact values from the chart/table.
• Break Down the Steps: Multi-part calculations? Solve them in stages.
• Estimate Smartly: Great for eliminating extremes, especially when choices are far apart.
• Ignore Irrelevant Data: Don’t get distracted — focus only on what the question asks.
• Understand the Visual: Read all titles, legends, footnotes, and axes labels.
• Sketch Mini-Tables: For complex charts, simplify on scratch paper to stay organized.

Now that we’ve covered each question type with examples, here are some overall strategies to maximize your GRE Quant score

1. Know Your Weak Spots

Use practice tests to identify which question types trip you up — Quantitative Comparison? Data Interpretation? Focus your prep there and ask yourself: Is it the math or the method that's holding me back?

2. Master the Basics

Brush up on key concepts like averages, ratios, area formulas, and percent changes. A strong foundation helps you tackle even tricky problems with confidence.

3. Simulate Test Conditions

Practice under timed conditions. Spend no more than 2 minutes per question — skip tough ones and come back later if needed.

4. Use the Calculator Wisely

It’s handy but basic. Use it for messy math, but don’t rely on it blindly. Always sanity-check your answers — especially for probability or decimals.

5. Learn From Every Mistake

Review why you missed a question: Did you misread? Make a math error? Miss a trick? Catching patterns in your mistakes = faster improvement.

6. Stay Calm, Stay Focused

Stress kills performance. Don’t panic if Section 2 feels harder — that means you did well on Section 1! Guess and move on when stuck.

7. Don’t Fear Hard Questions

You don’t need to get every hard question right to score high. Focus on nailing the medium-difficulty ones consistently — they matter more.